背景介绍

最近，期待已久的期权数据在聚宽上线了。我们可以在写有关期权策略的时候，直接调用实时行情和tick数据。为了让小伙伴们更加的了解期权，我在这里简单的描写了有关期权的定价模型和隐含波动率的计算方法。

期权作为金融创新的一种衍生金融工具，随着现代金融行业的逐步发展和成熟，在资产保值、套利、投机等方面发挥着重要作用，也促使金融资产定价的合理性和市场的繁荣。1973年美国芝加哥大学教授Fisher Black和斯坦福大学教授Myron Scholes在发表的论文《the pricing of options and Corporate Liabilities》中给出了经典的Black-Scholes期权定价模型，突破性的给出了欧式期权价格的明确解，并因此获得了诺贝尔经济学奖。

期权（OPTION）

期权（option）是基于标的资产（股票，利率，货币等）的衍生工具，是一种权益，赋予持有者在特定时间或时间段内以特定的价格买入或卖出标的资产的权利。基于期权行权的时间，可以将期权分为美式期权和欧式期权。美式期权可以在发行日与期权到期日这一段时间行权，而欧式期权只能在到期日那天行权。基于对标的资产的预测可以分为看涨期权和看跌期权。看涨期权（call option）是指可以按照特定价格买入标的资产的期权，看跌期权（put option）是指以特定价格卖出标的资产的期权。

期权定价模型

对于期权的定价方式，主要有两种。一种是传统的二叉树定价模型，一种就是本文所讲的经典的Black-Scholes期权定价模型。

Black-Scholes期权定价模型的市场假设

①没有交易成本和税费

②资产价格以连续随机方式运动

③空头卖出没有限制（允许借卖）

④资产没有中间阶段的现金流（如股利）

⑤没有无风险的套利机会存在

⑥标的资产价格符合Black-Scholes-Merton模型（几何布朗运动随机过程）

模型推导（风险中性定价原理（Risk-neutral valuation））

波动率

在实际的使用过程中，由于模型参数中的波动率delta并非常数，理论的期权价格和实际的期权价格存在误差。波动率是金融经济学中一个极其重要却又未知的一个变量，在资产定价、投资组合、风险管理及制定货币政策等方面发挥着极其重要的作用。因此准确的预测波动率成为关键，现在的研究方向主要分为两个方向。一是通过对历史波动率进行时间序列建模分析进行预测；二是隐含波动率法，利用期权现价求得BS隐含波动率（根据Black-Scholes期权定价模型求得）或者无模型隐含波动率（model-free implied volatility）

BS隐含波动率计算

本文使用经典的Newton-Raphson迭代法计算BS隐含波动率

模型的部分代码展示：

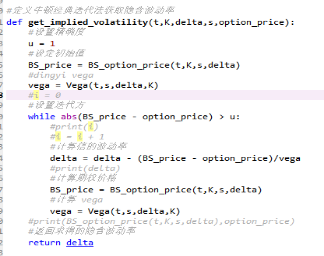
本文所写基于之前对期权的了解，希望对期权感兴趣的童鞋可以起到一定的作用，也欢迎大家对内容的建议。如果可以的话，希望可以和大家一起建立一个小群，专门讨论基于聚宽平台的期权策略及期权相关的知识。